Az Arduino játszótér 2018. december 31-től csak olvasható.

Bitmatemaitika oktatóanyag CosineKitty-től

Megjegyzés: Ezt az oldalt az Arduino fórumon lezajlott beszélgetés ihlette.

Tartalomjegyzék

Bevezető
A bináris rendszer
Bitenkénti ÉS
Bitenkénti VAGY
Bitenkénti KIZÁRÓ VAGY
Bitenkénti NEM
Biteltolás operátorok
Hozzárendelés operátorok
Figyelmeztetés: bitenkénti operátorok kontra logikai operátorok
Mindent összerakva: általános problémák megoldása

Néhány szó az Atmega8 mikrokontroller portregisztereiről
Haladó példa: megszakítás letiltása
Memória megtakarítása több adatelem egyetlen bájtba való becsomagolásával

Gyors referencia

Bevezető

Amikor Arduino környezetben (vagy bármilyen számítógépen) programozunk, gyakran a bitek egyedi kezelésének képessége ügyessé, sőt szükségessé válik. Íme néhány helyzet, amikor a bitmatematika hasznos lehet:

Memória megtakarítása akár 8 true/false adatérték egyetlen bájtba való becsomagolásával.
Egyes bitek be- és kikapcsolása egy vezérlőregiszterben vagy hardver-portregiszterben.
Bizonyos aritmetikai műveletek végrehajtása, beleértve a 2 hatványaival való szorzást vagy osztást.

Ebben az oktatóanyagban először a C++ nyelven elérhető alapvető bitenkénti operátorokat fedezzük fel. Ezután megtanuljuk, hogyan kombinálhatjuk őket bizonyos általános műveletek ügyes végrehajtásához.

A bináris rendszer

A bitenkénti operátorok jobb magyarázata érdekében ez az oktatóanyag a legtöbb egész értéket bináris megjelöléssel, más néven kettes alapú számrendszerben fejezi ki. Ebben a rendszerben minden egész érték csak a 0 és az 1 értéket használja minden számjegyhez. Gyakorlatilag minden modern számítógép belsőleg így tárolja az adatokat. Minden 0 vagy 1 számjegyet bitnek neveznek, ami a bináris számjegy (binary digit) rövidítése.

Az ismert decimális rendszerben (tízes alapú) egy olyan szám, mint az 572, azt jelenti, hogy 5*10² + 7*10¹ + 2*10⁰. Hasonlóképpen, binárisan egy olyan szám, mint az 11010 azt jelenti, hogy 1*2⁴ + 1*2³ + 0*2² + 1*2¹ + 0*2⁰ = 16 + 8 + 2 = 26.

Alapvető fontosságú, hogy megértse a bináris rendszer működését, hogy követhesse az oktatóanyag további részét. Ha segítségre van szüksége ezen a területen, egy jó kiindulópont a Wikipédia bináris rendszerről szóló cikke.

Az Arduino lehetővé teszi bináris számok megadását úgy, hogy 0b előtagot ír elő, pl. 0b11 == 3. Öröklődési okokból meghatározzhatja az állandókat B0-tól B11111111-ig jelöléssel, amelyek ugyanúgy használhatók.

Bitenkénti ÉS

A bitenkénti ÉS operátor a C++-ban egyetlen & jel, amelyet két másik egész kifejezés között használnak. A bitenkénti ÉS a kifejezések minden bitpozícióján egymástól függetlenül működik, a következő szabálynak megfelelően: ha mindkét bemeneti bit 1, a kapott kimenet 1, ellenkező esetben a kimenet 0. Másképp kifejezve:

    0 & 0 == 0
    0 & 1 == 0
    1 & 0 == 0
    1 & 1 == 1

Az Arduinóban az int típus 16 bites érték, így a & használata két int kifejezés között 16 egyidejű ÉS műveletet eredményez. Egy kódrészletben, például:

    int a =  92;    // binárisan:   0000000001011100
    int b = 101;    // binárisan:   0000000001100101
    int c = a & b;  // az eredmény: 0000000001000100, vagy 68 decimális.

Az a és b 16 bitje mindegyikét a bitenkénti ÉS módszerrel dolgozza fel, és mind a 16 eredményül kapott bitet a rendszer c-ben tárolja, így binárisan 01000100 lesz, ami decimálisan 68.

A bitenkénti ÉS egyik leggyakoribb felhasználási módja egy adott bit (vagy bitek) kiválasztása egy egész értékből, amit gyakran maszkolásnak neveznek. Például, ha egy x változó legkisebb helyiértékű bitjét szeretné elérni, és a bitet egy másik y változóban szeretné tárolni, használhatja a következő kódot:

    int x = 5;       // binárisan: 101
    int y = x & 1;   // most y == 1
    x = 4;           // binárisan: 100
    y = x & 1;       // most y == 0

Bitenkénti VAGY

A bitenkénti VAGY operátor a C++ nyelvben a függőleges vonal szimbólum, |. Mint a & operátor, | az egyes biteken egymástól függetlenül működik két egész kifejezésben, de amit csinál, az más (természetesen). Két bit bitenkénti VAGY értéke 1, ha az egyik vagy mindkét bemeneti bit 1, ellenkező esetben 0. Más szóval:

    0 | 0 == 0
    0 | 1 == 1
    1 | 0 == 1
    1 | 1 == 1

Íme egy példa a C++ kódrészletben használt bitenkénti VAGY-ra:

    int a =  92;    // binárisan:   0000000001011100
    int b = 101;    // binárisan:   0000000001100101
    int c = a | b;  // az eredmény: 0000000001111101, vagy 125 decimálisan.

A bitenkénti VAGYot gyakran használják annak biztosítására, hogy egy adott bit be legyen kapcsolva (1-re legyen állítva) egy adott kifejezésben. Például a bitek a-ból b-be másolásához, miközben ügyel arra, hogy a legkisebb helyiértékű bit 1-re legyen állítva, használja a következő kódot:

    b = a | 1;

Bitenkénti KIRÁRÓ VAGY

Van egy kissé szokatlan operátor a C++-ban, az úgynevezett bitenkénti KIZÁRÓ VAGY, más néven bitenkénti XOR. (Az angolban ezt általában "eksz-or"-nak ejtik.) A bitenkénti XOR operátort a ^ "kalap" szimbólummal írjuk. Ez az operátor hasonló a bitenkénti VAGY | operátorhoz, azzal a különbséggel, hogy 1-re értékeli ki az adott pozíciót, ha az adott pozícióhoz tartozó bemeneti bitek közül pontosan egy 1. Ha mindkettő 0 vagy mindkettő 1, az XOR operátor 0-ra értékelődik ki:

    0 ^ 0 == 0
    0 ^ 1 == 1
    1 ^ 0 == 1
    1 ^ 1 == 0

A bitenkénti XOR egy másik értelmezési módja az, hogy az eredmény minden bitje 1, ha a bemeneti bitek különböznek, vagy 0, ha azonosak.

Íme egy egyszerű kódpélda:

    int x = 12;     // binárisan: 1100
    int y = 10;     // binárisan: 1010
    int z = x ^ y;  // binárisan: 0110, vagy decimálisan 6

A ^ operátort gyakran használják az egész kifejezés egyes bitjeinek átváltására (vagyis 0-ról 1-re vagy 1-re 0-ra történő megváltoztatására), míg másokat magukra hagynak. Például:

    y = x ^ 1;   // kapcsolja át a legkisebb helyiértékű bitet x-ben, és az eredményt y-ban tárolja.

Bitenkénti NEM

A bitenkénti NEM operátor a C++-ban a ~ tilde karakter.A & és |-től eltérően a bitenkénti NEM operátor a tőle jobbra lévő egyetlen operandusra vonatkozik. A bitenkénti NEM minden bitet az ellenkezőjére változtat: a 0-ból 1 lesz, az 1-ből pedig 0. Például:

    int a = 103;    // binárisan:  0000000001100111
    int b = ~a;     // binárisan:  1111111110011000 = -104

Meglepődhet, ha a művelet eredményeként negatív számot lát, például -104. Ennek az az oka, hogy az int változó legmagasabb helyiértékű bitje az úgynevezett előjelbit. Ha a legmagasabb bit 1, akkor a szám negatívként értelmeződik. A pozitív és negatív számoknak ezt a kódolását kettes komplementernek nevezik. További információkért lásd a Wikipédia kettes komplementer című cikkét.

Félretéve, érdekes megjegyezni, hogy bármely x egész szám esetén ~x ugyanaz, mint -x - 1.

Időnként az előjeles egész kifejezésben lévő jelbit nem kívánt meglepetéseket okozhat, amint azt később látni fogjuk.

Biteltolás operátorok

Két biteltolás operátor van a C++-ban: a balra eltolás operátor << és a jobbra eltolás operátor >>. Ezek az operátorok a bal oldali operandus bitjeit balra vagy jobbra tolják el a jobb oldali operandus által meghatározott számú pozícióval. Például:

    int a = 5;        // binárisan: 0000000000000101
    int b = a << 3;   // binárisan: 0000000000101000, vagy 40 decimálisan
    int c = b >> 3;   // binárisan: 0000000000000101, vagy vissza az 5-re, ahogy kezdtük

Ha egy x értéket y bittel tol el (x << y), akkor az x bal szélső y db bitje elveszik, szó szerint kitolódik a létezésből:

    int a = 5;        // binárisan: 0000000000000101
    int b = a << 14;  // binárisan: 0100000000000000 - az első 1-es a 101-ből elveszik

Ha biztos abban, hogy az értékek egyike sem tolódik el a feledés homályába, akkor a balra eltolás operátort egyszerűen úgy képzelheti el, hogy a bal oldali operandust megszorozza 2-vel a jobb operandus hatványára emelve. Például 2 hatványainak generálásához a következő kifejezések használhatók:

    1 <<  0  ==    1
    1 <<  1  ==    2
    1 <<  2  ==    4
    1 <<  3  ==    8
    ...
    1 <<  8  ==  256
    1 <<  9  ==  512
    1 << 10  == 1024
    ...

Ha x-et y bittel (x >> y) jobbra tolja, és az x-ben a legmagasabb helyiértékű bit 1-es, a viselkedés az x pontos adattípusától függ. Ha x int típusú, akkor a legmagasabb bit az előjelbit, amely meghatározza, hogy x negatív-e vagy sem, amint azt fentebb tárgyaltuk. Ebben az esetben ezoterikus történelmi okokból az előjelbitet alacsonyabb bitekre másolják:

    int x = -16;     // binárisan: 1111111111110000
    int y = x >> 3;  // binárisan: 1111111111111110

Ez a jelkiterjesztésnek nevezett viselkedés gyakran nem a kívánt viselkedés. Ehelyett azt kívánhatja, hogy a nullákat balról tolja el. Kiderült, hogy a jobb oldali eltolási szabályok eltérőek az unsigned int kifejezéseknél, így típusátalakítás segítségével elnyomhatja a balról másolandókat:

    int x = -16;               // binárisan: 1111111111110000
    int y = unsigned(x) >> 3;  // binárisan: 0001111111111110

Ha ügyel arra, hogy elkerülje a jelek kiterjesztését, használhatja a >> jobbra váltó operátort a 2 hatványaival való osztáshoz. Például:

    int x = 1000;
    int y = x >> 3;   // 1000 egész osztása 8-cal, ami y = 125-öt eredményez.

Hozzárendelés operátorok

A programozás során gyakran egy x változó értékével akarunk operálni, és a módosított értéket visszamenteni x-be. A legtöbb programozási nyelvben például a következő kóddal növelheti az x változó értékét 7-tel:

    x = x + 7;    // növeld x-et 7-tel

Mivel az ilyesmi gyakran előfordul a programozásban, a C++ gyorsírást biztosít speciális hozzárendelési operátorok formájában. A fenti kódrészlet tömörebben is felírható így:

    x += 7;    // növeld x-et 7-tel

Kiderül, hogy a bitenkénti ÉS, a bitenkénti VAGY, a balra eltolás és a jobbra eltolás mindegyikének van gyorsított hozzárendelési operátora. Íme egy példa:

    int x = 1;  // binárisan: 0000000000000001
    x <<= 3;    // binárisan: 0000000000001000
    x |= 3;     // binárisan: 0000000000001011 - mert a 3 11 binárisan
    x &= 1;     // binárisan: 0000000000000001
    x ^= 4;     // binárisan: 0000000000000101 - átváltás 100 bináris maszk használatával
    x ^= 4;     // binárisan: 0000000000000001 - visszaváltás 100 bináris maszk használatával

Nincs gyorsírási hozzárendelési operátor a bitenkénti NOT operátorhoz ~; Ha az x összes bitjét át szeretné váltani, akkor ezt kell tennie:

    x = ~x;    // kapcsolja át az összes bitet x-ben, és tárolja vissza x-ben

Figyelmeztetés: bitenkénti operátorok kontra logikai operátorok

Nagyon könnyű összetéveszteni a C++ bitenkénti operátorait a logikai operátorokkal. Például a bitenkénti ÉS & operátor nem egyezik meg a logikai ÉS && operátorral, két okból:

Nem ugyanúgy számítják ki a számokat. Bitenkénti & függetlenül működik az operandusai minden bitjén, míg az && mindkét operandusát logikai értékké alakítja (true==1 vagy false==0), majd egyetlen true vagy false értéket ad vissza. Például, 4 & 2 == 0, mert a 4 az 100 binárisan és a 2 az 010 binárisan, és nincs 1-es a két számban ugyanazon a helyiértéken. Azonban 4 && 2 == true, és a true számszerűen egyenlő 1-gyel. Ennek az az oka, hogy a 4 nem 0, és a 2 nem 0, így mindkettő logikai true értéknek minősül.
A bitenkénti operátorok mindig mindkét operandusukat értékelik, míg a logikai operátorok úgynevezett short-cut kiértékelést használnak. Ez csak akkor számít, ha az operandusoknak vannak mellékhatásai, például kimenetet idéznek elő, vagy megváltoztatják valami más értékét a memóriában. Íme egy példa arra, hogy két hasonló kinézetű kódsor viselkedése nagyon eltérő lehet:

    int fred (int x)
    {
        Serial.print ("fred ");
        Serial.println (x, DEC);
        return x;
    }

    void setup()
    {
        Serial.begin (9600);
    }

    void loop()
    {
        delay(1000);    // várj 1 másodpercet, így a kimenetet nem árasztják el soros adatok!
        int x = fred(0) & fred(1);
    }

Ha lefordítja és feltölti ezt a programot, majd figyeli az Arduino GUI soros kimenetét, akkor a következő szövegsorokat fogja látni másodpercenként ismétlődően:

    fred 0
    fred 1

Ennek az az oka, hogy a fred(0) és a fred(1) is meghívásra kerül, így a generált kimenet eredményeként a 0 és 1 visszatérési értékek bitenkénti ÉS kapcsolatba kerülnek, majd a 0 értéke x-ben tárolódik. Ha átszerkeszti a

        int x = fred(0) & fred(1);

sort és kicseréli a bitenkénti &-t logikai megfelelőjére &&,

        int x = fred(0) && fred(1);

és fordítsa le, töltse fel és futtassa újra a programot, meglepődhet, ha a soros monitor ablakában másodpercenként csak egyetlen szövegsor ismétlődik:

    fred 0

Miért történik ez? Ez azért van, mert a logikai && short-cut-ot használ: ha a bal oldali operandusa nulla (azaz false), akkor már biztos, hogy a kifejezés eredménye false lesz, így nem kell kiértékelni a jobb oldali operandust. Más szavakkal, a kódsor int x = fred(0) && fred(1); jelentésében azonos:

    int x;
    if (fred(0) == 0) {
        x = false;  // 0-t tárol x-ben
    } else {
        if (fred(1) == 0) {
            x = false;  // 0-t tárol x-ben
        } else {
            x = true;   // 1-t tárol x-ben
        }
    }

Nyilvánvaló, hogy a logikai && sokkal tömörebb módja ennek a meglepően összetett logikának.

Akárcsak a bitenkénti ÉS és a logikai AND esetén, vannak különbségek a bitenkénti VAGY és a logikai VAGY között is. A bitenkénti VAGY operátor | mindig mindkét operandust kiértékeli, míg a logikai VAGY operátor || csak akkor értékeli ki a jobb oldali operandusát, ha a bal oldali operandusa false (nulla). Továbbá, bitenkénti | az operandusok minden bitjén függetlenül működik, míg a logikai || mindkét operandusát true-nak (nem nulla) vagy false-nak (nulla) kezeli, és vagy true-ra (ha valamelyik operandus nem nulla) vagy false-ra (ha mindkét operandus nulla) értékeli ki.

Mindent összerakva: általános problémák megoldása

Most elkezdjük megvizsgálni, hogyan kombinálhatjuk a különféle bitenkénti operátorokat, hogy hasznos feladatokat hajtsanak végre C++ szintaxis használatával Arduino környezetben.

Néhány szó az Atmega8 mikrokontroller portregisztereiről

Általában amikor az Atmega8 digitális kivezetéseiről szeretne olvasni vagy írni, akkor az Arduino környezet által biztosított beépített digitalRead() vagy digitalWrite() függvényeket használja. Tegyük fel, hogy a setup() függvényben a 2-től 13-ig terjedő digitális kivezetéseket akarta definiálni kimenetként, majd azt akarta, hogy a 11-es, 12-es és 13-as kivezetések HIGH-ra legyenek állítva, az összes többi kivezetés pedig LOW-ra. Általában a következőképpen lehet ezt elérni:

    void setup()
    {
        int pin;
        for (pin=2; pin <= 13; ++pin) {
            pinMode (pin, OUTPUT);
        }
        for (pin=2; pin <= 10; ++pin) {
            digitalWrite (pin, LOW);
        }
        for (pin=11; pin <= 13; ++pin) {
            digitalWrite (pin, HIGH);
        }
    }

Kiderül, hogy van egy másik lehetőség ugyanerre, az Atmega8 hardverportokhoz való közvetlen hozzáféréssel és bitenkénti operátorokkal:

    void setup()
    {
        // állítsa be kimenetnek az 1-es (soros adás)
        // és a 2..7 lábat, de hagyja a 0-s lábat (soros vétel)
        // bemenetnek (ellenkező esetben a soros port nem működik!) ... 
        DDRD = B11111110;  // digitális kivezetések: 7,6,5,4,3,2,1,0

        // 8..13 kivezetések beállítása output-ra...
        DDRB = B00111111;  // digitális kivezetések: -,-,13,12,11,10,9,8

        // Kapcsolja ki a digitális kimeneti 2..7 kivezetéseket  ...
        PORTD &= B00000011;   // kikapcsolja a 2..7 kivezetéseket, de változatlanul hagyja a 0-as és 1-es kivezetéseket

        // Egyidejű írás a 8..13 kivezetésekre ...
        PORTB = B00111000;   // bekapcsolja 13,12,11-et; kikapcsolja a 10,9,8-at
    }

Ez a kód azt a tényt használja ki, hogy a DDRD és DDRB vezérlőregiszterek egyenként 8 bitet tartalmaznak, amelyek meghatározzák, hogy egy adott digitális kivezetés kimenet (1) vagy bemenet (0) legyen. A DDRB felső 2 bitje nincs használva, mert az Atmega8-on nincs 14-es vagy 15-ös digitális kivezetés. Hasonlóképpen, a PORTB és PORTD portregiszterek egy bitet tartalmaznak az egyes digitális kivezetésekhez legutóbb írt értékhez, HIGH (1) vagy LOW (0).

Általánosságban elmondható, hogy az ilyesmi nem jó ötlet. Miért nem? Íme néhány ok:

A kódot sokkal nehezebb benne hibát keresni és karbantartani, mások számára pedig sokkal nehezebb megérteni. A processzornak csak néhány mikroszekundum kell a kód végrehajtásához, de órákba telhet, amíg rájön, hogy miért nem működik megfelelően, és kijavítja! Az időd értékes, igaz? De a számítógép ideje nagyon olcsó, az általad betáplált áram árában mérve. Általában sokkal jobb, ha a kódot a legkézenfekvőbb módon írjuk le.
A kód kevésbé hordozható. A digitalRead() és digitalWrite() használata esetén sokkal könnyebb olyan kódot írni, amely az összes Atmel mikrokontrolleren fut, míg a vezérlő- és portregiszterek eltérőek lehetnek az egyes mikrokontrollereken.
Közvetlen port-hozzáféréssel sokkal könnyebb véletlen meghibásodásokat okozni. Figyelje meg, hogy a DDRD = B11111110; sort; fent megemlítettük, hogy a 0-t kell hagynia bemeneti kivezetésként. A 0. kivezetés a vételi vonal a soros porton. Nagyon könnyű lenne véletlenül leállítani a soros portot úgy, hogy a 0-s kivezetést kimeneti kivezetésre cseréljük! Az nagyon zavaró lenne, ha hirtelen nem tudna soros adatokat fogadni, nem igaz?

Szóval lehet, hogy azt mondod magadnak, nagyszerű, miért akarnám akkor valaha is használni ezt a cuccot? Íme a közvetlen port-elérés néhány pozitív oldala:

Ha kevés a programmemória, ezekkel a trükkökkel csökkentheti a kódot. Sokkal kevesebb bájt lefordított kódra van szükség ahhoz, hogy egy csomó hardver kivezetést egyidejűleg írjunk a portregisztereken keresztül, mint a for ciklus használatával az egyes kivezetések külön beállításához. Bizonyos esetekben ez különbség lehet a között, hogy a program elfér-e a flash memóriában, vagy sem!
Előfordulhat, hogy egyszerre több kimeneti kivezetést kell beállítania. digitalWrite(10,HIGH); hívása; ezt követi a digitalWrite(11,HIGH); A 10-es érintkező a 11-es érintkező előtt néhány mikromásodperccel HIGH-ra fog menni, ami összezavarhat bizonyos időérzékeny külső digitális áramköröket, amelyeket csatlakoztatott. Alternatív megoldásként mindkét kivezetést pontosan ugyanabban az időpontban állíthatja magasra a PORTB |= B1100; használatával.
Előfordulhat, hogy a kivezetéseket nagyon gyorsan, vagyis a mikroszekundum töredékén belül kell be- és kikapcsolni.Ha megnézzük a forráskódot a lib/targets/arduino/wiring.c fájlban, látni fogjuk, hogy a digitalRead() és a digitalWrite() egy tucatnyi kódsor, amelyekből jónéhány gépi utasítás kerül lefordításra.Minden gépi utasításhoz egy órajelciklus szükséges 16 MHz-en, ami az időérzékeny alkalmazásokban összeadódik.A közvetlen port-hozzáférés sokkal kevesebb órajellel képes elvégezni ugyanazt a munkát.

Haladó példa: megszakítás letiltása

Most pedig vegyük a tanultakat, és kezdjük el megérteni azokat a furcsa dolgokat, amelyeket a haladó programozók csinálnak néha a kódjukban. Mit jelent például, ha valaki a következőket teszi?

      // A megszakítás letiltása.
      GICR &= ~(1 << INT0);

Ez egy tényleges kódminta az Arduino 0007 runtime könyvtárából, a lib\targets\arduino\winterrupts.c fájlban. Először is tudnunk kell, mit jelent a GICR és az INT0. Kiderül, hogy a GICR egy vezérlőregiszter, amely meghatározza, hogy bizonyos CPU megszakítások engedélyezettek (1) vagy letiltottak (0). Ha az Arduino szabványos fejlécfájljai között keresünk az INT0 számára, különféle definíciókat találunk. Attól függően, hogy milyen mikrokontrollerhez írsz, lehet

    #define INT0   6

vagy

    #define INT0   0

Tehát egyes processzorokon a fenti kódsor a következőre fordul:

    GICR &= ~(1 << 0);

és másokon a következőkre fordítja:

    GICR &= ~(1 << 6);

Vizsgáljuk meg az utóbbi esetet, mert ez szemléletesebb. Először is, az (1 << 6) érték azt jelenti, hogy az 1-et 6 bittel balra toljuk, ami megegyezik a 2⁶-nal vagyis 64-gyel. Ebben az összefüggésben hasznosabb, ha ezt az értéket binárisan látjuk: 01000000. Ezután a ~ bitenkénti NEM operátor kerül alkalmazásra erre az értékre, ami az összes bit átváltását eredményezi: 10111111. Ekkor a bitenkénti ÉS hozzárendelési operátor kerül felhasználásra, így a fenti kódnak ugyanaz a hatása, mint:

    GICR = GICR & B10111111;

Ennek az a hatása, hogy az összes bit változatlanul marad a GICR-ben, kivéve a legmagasabbtól a második bit, amely ki lesz kapcsolva.

Abban az esetben, ha az INT0 0-ra lett definiálva az adott mikrokontrollernél, a kódsor ehelyett úgy értelmeződik, mint:

    GICR = GICR & B11111110;

ami kikapcsolja a legalacsonyabb bitet a GICR regiszterben, de a többi bitet úgy hagyja, ahogy volt. Ez egy példa arra, hogyan tud az Arduino környezet a mikrokontrollerek széles skáláját támogatni a runtime könyvtár egyetlen sorának forráskódja.

Memória megtakarítása több adatelem egyetlen bájtba való becsomagolásával

Sok olyan helyzet van, amikor sok adatértékkel rendelkezik, amelyek mindegyike true vagy false lehet. Példa erre, ha saját LED-rácsot épít, és szimbólumokat szeretne megjeleníteni a rácson az egyes LED-ek be- vagy kikapcsolásával. Egy példa egy 5x7-es bittérképre az X betűhöz így nézhet ki:

Egy ilyen kép tárolásának egyszerű módja egész számok tömbjének használata. Ennek a megközelítésnek a kódja így nézhet ki:

    const prog_uint8_t BitMap[5][7] = {   // tárolás a program memóriájában a RAM mentéséhez
        {1,1,0,0,0,1,1},
        {0,0,1,0,1,0,0},
        {0,0,0,1,0,0,0},
        {0,0,1,0,1,0,0},
        {1,1,0,0,0,1,1}
    };

    void DisplayBitMap()
    {
        for (byte x=0; x<5; ++x) {
            for (byte y=0; y<7; ++y) {
                byte data = pgm_read_byte (&>BitMap[x][y]);   // adatok lekérése a program memóriájából
                if (data) {
                    // kapcsolja be a LED-et az (x,y) helyen
                } else {
                    // kapcsolja ki a LED-et az (x,y) helyen
                }
            }
        }
    }

Ha ez lenne az egyetlen bittérkép a programjában, ez egyszerű és hatékony megoldás lenne a problémára. 1 bájt programmemóriát használunk (ebből kb. 7K áll rendelkezésre az Atmega8-ban) a bittérképünk minden pixeléhez, összesen 35 bájtot. Ez nem olyan rossz, de mi van, ha bittérképet szeretne az ASCII-karakterkészlet mind a 96 nyomtatható karakteréhez? Ez 96*35 = 3360 bájtot fogyasztana, ami sokkal kevesebb flash memóriát hagyna a programkód tárolására.

Létezik egy sokkal hatékonyabb módja a bittérképek tárolásának. Cseréljük le a fenti 2-dimenziós tömböt egy 1-dimenziós bájttömbre.Minden bájt 8 bitet tartalmaz, és mindegyikből a legalacsonyabb 7 bitet fogjuk használni az 5x7-es bittérképünk oszlopában lévő 7 pixel ábrázolására:

    const prog_uint8_t BitMap[5] = {   // tárolás a program memóriájában a RAM mentéséhez
        B1100011,
        B0010100,
        B0001000,
        B0010100,
        B1100011
    };

(Itt az Arduino 0007-től kezdve elérhető, előre meghatározott bináris konstansokat használjuk.) Ez lehetővé teszi, hogy 35 helyett 5 bájtot használjunk minden bittérképhez. De hogyan használjuk ki ezt a kompaktabb adatformátumot? Itt a válasz: átírjuk a DisplayBitMap() függvényt, hogy elérjük a BitMap egyes bájtjaiban lévő egyes biteket...

    void DisplayBitMap()
    {
        for (byte x=0; x<5; ++x) {
            byte data = pgm_read_byte (&BitMap[x]);   // adatok lekérése a program memóriájából
            for (byte y=0; y<7; ++y) {
                if (data & (1<<y)) {
                    // kapcsolja be a LED-et az (x,y) helyen
                } else {
                    // kapcsolja ki a LED-et az (x,y) helyen
                }
            }
        }
    }

A döntő sor a megértéshez

    if (data & (1<<y)) {

Az (1<<y) kifejezés kiválaszt egy adott bitet a data-n belül, amelyeket el szeretnénk érni. Ezután bitenkénti ÉS használatával a data & (1<<y) teszteli az adott bitet. Ha ez a bit be van állítva, akkor nullától eltérő értéket kapunk, ami miatt az if igaznak látja. Ellenkező esetben, ha a bit nulla, akkor a rendszer hamisként kezeli, így az else hajtódik végre.

Gyors referencia

Ebben a gyorsreferenciában egy 16 bites egész szám bitjeire a legkisebb helyiértékű bitre 0. bitként hivatkozunk, a legnagyobb helyiértékű bitre (az előjelbitre, ha az egész szám előjeles) pedig a 15. bitre hivatkozunk, amint az ezen az ábrán látható:

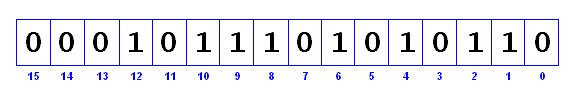
Bármikor az n változót látja, az értéke 0 és 15 között van.

    y = (x >> n) & 1;    // n=0..15.  x n-edik bitjét tárolja y-ban. y 0-át vagy 1-et kap.

    x &= ~(1 << n);      // x n-edik bitjét 0-ra kényszeríti. Az összes többi bit változatlan marad.

    x &= (1<<(n+1))-1;   // változatlanul hagyja x legkisebb n bitjét; minden magasabb bit 0 lesz.

    x |= (1 << n);       // x n-edik bitjét 1-re kényszeríti. Az összes többi bit változatlan marad.

    x ^= (1 << n);       // átállítja x n. bitjét. Az összes többi bit változatlan marad.

    x = ~x;              // átállítja x ÖSSZES bitjét.

Itt van egy érdekes függvény, amely bitenkénti & és logikai && függvényeket is használ. Akkor és csak akkor ad vissza igazat, ha az adott 32 bites x egész szám 2 tökéletes hatványa, azaz 1, 2, 4, 8, 16, 32, 64 stb. Például az IsPowerOfTwo(64) hívása true, de az IsPowerOfTwo(65) false értéket ad vissza. A függvény működésének megtekintéséhez használjuk a 64-es számot 2 hatványának példájaként. Binárisan a 64 1000000. Ha 1000000-ből kivonunk 1-et, 0111111-et kapunk. A bitenkénti & alkalmazásával az eredmény 0000000. De ha ugyanezt tesszük a 65-tel (bináris 1000001), akkor 1000001 & 1000000 == 1000000, ami nem nulla.

    bool IsPowerOfTwo (long x)
    {
        return (x > 0) && (x & (x-1) == 0);
    }

Itt van egy függvény, amely megszámolja, hogy a 16 bites x egész szám hány bitje 1, és visszaadja a számot:

    int CountSetBits (int x)
    {
        int count = 0;
        for (int n=0; n<16; ++n) {
            if (x & (1<<n)) {
                ++count;
            }
        }
        return count;
    }

Egy másik módja ugyanennek:

    int >CountSetBits (int x)
    {
        unsigned int count;
        for (count = 0; x; count++)
            x &= x - 1; 
        return count;
    }

Különféle trükkök találhatók a gyakori bitorientált műveletekhez itt.